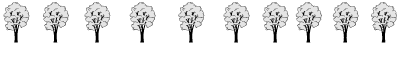Der Einzelne
- Denk-Muster Wahrnehmung von Wirklichkeit Arbeitsweisen des Gehirns Kreativität und Ethik Denkfehler Kreativitätsblockaden Auswege Übung macht den Meister Trainingsmöglichkeiten

Übung macht den Meister

Seite 1: Denk-Muster-Übungen

Jeder Mensch denkt in angelernten, ihm vertrauten Mustern, Strukturen oder Schablonen, die ihm als geistige »Trampelpfade« kaum bewusst sind. Deshalb sind es für ihn die einzig möglichen und »richtigen« Denkweisen.

Nichts gegen bequeme »geistige Trampelpfade«, solange wir erkennen, wann sie zum Irrweg bzw. zum geistigen Gefängnis werden. Das Beispiel von Klein-Eva bzw. der Oma und dem Laufstall im Abschnitt »Was ist kreatives Denken?« illustriert dies sehr deutlich. Zum Erkennen und Überwinden von starren Denk-Mustern gibt, es eine Fülle von Literatur, die dies in Theorie und Praxis vertieft. Sie lädt ein zum Üben und Trainieren.

Um zu zeigen, dass dies kein philosophisches sondern ein reales Problem von »Jedermann« ist, werden als kleine Auswahl zehn Denk-Muster-Übungen angeboten.

Aufgabe 1

Erkennen Sie das Muster nebenstehender drei Zeichenfolgen und fügen Sie das logisch Nachfolgende an.

zur Lösung

Aufgabe 2

Lassen sich diese neun Punkte mit vier geraden Linien in einem Zug (also ohne Stift abzusetzen) verbinden.

zur Lösung

Aufgabe 3

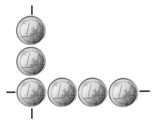
Erreichen Sie, daß durch das Umlegen eines Eurostückes anschließend auf jeder Achse 4 Eurostücke zu liegen kommen.

zur Lösung

Aufgabe 4

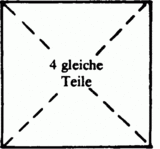
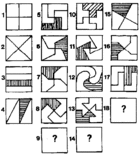
Wie viele Lösungen (Alternativen) gibt es, das Quadrat in 4 gleichgroße (deckungsgleiche) Teile zu teilen?

zur Lösung

Aufgabe 5

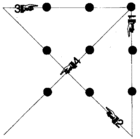
In einem Garten sollen 10 Bäume gepflanzt werden, die so anzuordnen sind, dass sie genau 5 Reihen mit jeweils 4 Bäumen ergeben.

zur Lösung

Aufgabe 6

Zwei Männer wollen bei Köln den Rhein überqueren. Das Boot, das am Ufer lag, bot nur Platz für eine Person. Beide überquerten den Rhein in diesem Boot und setzten anschließend ihre Reise fort. Wie konnten sie dies tun?

zur Lösung

Aufgabe 7

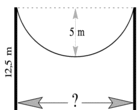
Zwischen zwei Pfosten, die je 12,50 m hoch sind, wird ein Seil gespannt, das 10 m lang ist, aber 5 m durchhängt. Wie weit stehen die beiden Pfosten auseinander?

zur Lösung

Aufgabe 8

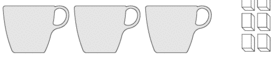
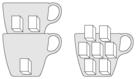
Deponieren Sie in drei Kaffeetassen 10 Zuckerwürfel, sodass in jeder Tasse eine ungerade Zahl von Würfeln liegt.

zur Lösung

Aufgabe 9

Die beiden Akrobaten Pitt (1,94m groß) und Pat (1,54m groß) gehen spazieren und sehen einen herrlichen, vollen Birnbaum. Da steigt Pat auf Pitts Schultern, um jedem eine Frucht zu holen. Er reicht jedoch nur bis auf 15cm an die Birnen heran. Wie können sie - ohne weitere Hilfsmittel doch noch an die leckeren Birnen kommen?

zur Lösung

Aufgabe 10

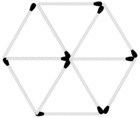
Bauer Alois baut sich aus 13 Gattern 6 gleichgroße Pferche für seine Schafe. Da zerstört ihm ein Sturm 1Gatter. Kann er aus den verbliebenen 12 Gattern wieder 6 gleichgroße Pferche bauen? Suchen Sie die Lösung mit Streichhölzern.

zur Lösung

Seite 2: Lösungen 1-5

Der »Schlüssel« zur Lösung ist immer der gleiche: Das gegebene, automatische, unbewusste Denk-Muster mit seiner Enge und seinen Grenzen erkennen, dann damit »spielen« und es ggf. wechseln. Wichtig ist auch, nicht bei der ersten besten Lösung stehen zu bleiben. Häufig gibt es mehrere und die »beste« setzt Auswahlmöglichkeiten voraus.

Zu Aufgabe 1:

Auf der Ebene des Systems »Alphabet« lassen sich auch andere Systeme, wie z.B. »Zahlen« oder »(Fremd-) Sprachen« ausdrücken.

1 3 5 7 9	(immer eine Zahl auslassen)
E Z D V F	(Eins, Zwei, Drei, Vier, Fünf, ...)
O T T F F	(One, Two, Three, Four, Five)

Zu Aufgabe 2:

Die äußeren Punkte markieren keine Systemgrenze! Bleibt man innerhalb dieser selbst angenommenen - jedoch nicht vorgegebenen - Grenze, findet man keine Lösung, überschreitet man sie, gibt es gleich mehrere.

Kreativitätstechniken – Lösung Aufgabe 2 — Anklicken zum Vergrößern

Zu Aufgabe 3:

Mit zweidimensionalem Denken nicht zu lösen, aber dreidimensional schon!

Aufgabe 4:

Unendliche viele Lösungsmöglichkeiten! Es gibt nicht nur gerade Linien, sondern auch (ein- und mehrfach) geknickte, sowie vielfältig geschwungene, die die Bedingung der Aufgabe ebenfalls erfüllen. Denkt man sich die Teilung vom Rand des Quadrates her, gibt es weniger Möglichkeiten, als wenn man vom Mittelpunkt aus denkt. Denkt man bei »Teilen« an Schneiden, fallen einem weniger Lösungen ein, als wenn man gedanklich von Malen oder Zeichnen ausgeht.

Kreativitätstechniken – Lösung Aufgabe 4 — Anklicken zum Vergrößern

Zu Aufgabe 5:

Die Anordnung muss so gewählt werden, dass jeder Baum doppelt zählt. Die Blockade besteht im Glauben an die mathematische Logik, die man nicht durchbrechen kann, und im Suchen nach einer rechtwinkligen Lösung.

Kreativitätstechniken – Lösung Aufgabe 5 — Anklicken zum Vergrößern

Seite 3: Lösungen 6-10

Zu Aufgabe 6:

Jeder der beiden kam von einer anderen Seite an den Rhein. Der Eine fand das Boot, setzte über, dann nahm der Andere das Boot und fuhr wieder zurück. Blockade: Die nicht vorhandene und daher selbstgesetzte Denk-Grenze, dass beide zusammen an dasselbe Rheinufer gekommen sind.

Kreativitätstechniken – Lösung Aufgabe 6 — Anklicken zum Vergrößern

Zu Aufgabe 7:

Die Pfosten stehen nebeneinander, wenn 10m Seil 5m durchhängen! Die nicht notwendige aber fehlerhafte Zeichnung (=ungeprüfte Übernahme der Ausgangslage) blockiert hier das logische Denken.

zu Aufgabe 8:

Die Blockade besteht in der selbstgesetzten Annahme, dass die Tassen immer separat stehen müssen. Die Lösung wird erst möglich, wenn diese unnötige Denk-Schablone aufgegeben wird.