Der »Schlüssel« zur Lösung ist immer der gleiche: Das gegebene, automatische, unbewusste Denk-Muster mit seiner Enge und seinen Grenzen erkennen, dann damit »spielen« und es ggf. wechseln. Wichtig ist auch, nicht bei der ersten besten Lösung stehen zu bleiben. Häufig gibt es mehrere und die »beste« setzt Auswahlmöglichkeiten voraus.
Zu Aufgabe 1:
Auf der Ebene des Systems »Alphabet« lassen sich auch andere Systeme, wie z.B. »Zahlen« oder »(Fremd-) Sprachen« ausdrücken.
|
1 3 5 7 9 |
(immer eine Zahl auslassen) |
|
E Z D V F |
(Eins, Zwei, Drei, Vier, Fünf, ...) |
|
O T T F F |
(One, Two, Three, Four, Five) |
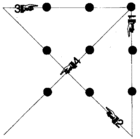
Zu Aufgabe 2:
Die äußeren Punkte markieren keine Systemgrenze! Bleibt man innerhalb dieser selbst angenommenen - jedoch nicht vorgegebenen - Grenze, findet man keine Lösung, überschreitet man sie, gibt es gleich mehrere.
Zu Aufgabe 3:
Mit zweidimensionalem Denken nicht zu lösen, aber dreidimensional schon!
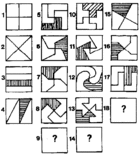
Aufgabe 4:
Unendliche viele Lösungsmöglichkeiten! Es gibt nicht nur gerade Linien, sondern auch (ein- und mehrfach) geknickte, sowie vielfältig geschwungene, die die Bedingung der Aufgabe ebenfalls erfüllen. Denkt man sich die Teilung vom Rand des Quadrates her, gibt es weniger Möglichkeiten, als wenn man vom Mittelpunkt aus denkt. Denkt man bei »Teilen« an Schneiden, fallen einem weniger Lösungen ein, als wenn man gedanklich von Malen oder Zeichnen ausgeht.
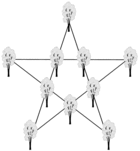
Zu Aufgabe 5:
Die Anordnung muss so gewählt werden, dass jeder Baum doppelt zählt. Die Blockade besteht im Glauben an die mathematische Logik, die man nicht durchbrechen kann, und im Suchen nach einer rechtwinkligen Lösung.